ประพจน์ คือ ประโยค หรือข้อความที่อยู่ในรูปแบบประโยคบอกเล่า หรือประโยคปฏิเสธ ที่เป็นจริงหรือเป็นเท็จอย่างใดอย่างหนึ่ง
ตัวอย่างเช่น
• ร้อยเอ็ดเป็นจังหวัดทางภาคกลาง → เป็นประพจน์ เพราะเป็นประโยคบอกเล่าที่เป็นเท็จ
• ใครไม่เข้าห้องเรียนคณิตศาสตร์ → ไม่เป็นประพจน์ เพราะเป็นประโยคคำถามและบอกไม่ได้ว่าเป็นจริงหรือเท็จ
• -9 ไม่เป็นจำนวนเต็มบวก → เป็นประพจน์ เพราะเป็นประโยคปฏิเสธที่มีค่าความจริงเป็นจริง
นั่นคือ ประโยคคำถาม คำสั่ง ขอร้อง คำอุทาน หรือประโยคที่ไม่สามารถระบุค่าความจริงได้ ไม่เป็นประพจน์
กำหนดให้ p และ q เป็นประพจน์ใดๆ
เราสามารถเชื่อมประพจน์ทั้งสองเข้าด้วยกันได้ โดยอาศัยตัวเชื่อมประพจน์ดังต่อไปนี้
1. ตัวเชื่อมประพจน์ "และ"
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ "และ" สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∧ q
ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงเป็นจริง (T) ทั้งคู่
นอกนั้นมีค่าความจริงเป็นเท็จ (F)
2. ตัวเชื่อมประพจน์ "หรือ"
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ "หรือ"
สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∨q ซึ่งจะมีค่าความจริงเป็นเท็จ (F)
เมื่อ p และ q มีค่าความจริงเป็นเท็จ (F) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นจริง (T)
3. ตัวเชื่อมประพจน์ "ถ้า...แล้ว"
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ "ถ้า...แล้ว"
สามารถเขียนแทนได้ด้วยสัญลักษณ์ p → q ซึ่งจะมีค่าความจริงเป็นเท็จ (F)
เมื่อ p เป็นจริง (T) และ q เป็นเท็จ (F) นอกนั้นมีค่าความจริงเป็นจริง (T)
4. ตัวเชื่อมประพจน์ "ก็ต่อเมื่อ"
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ "ก็ต่อเมื่อ"
สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ⇔ q ซึ่งจะมีค่าความจริงเป็นจริง (T)
เมื่อ p และ q มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ (F)
เมื่อ p และ q มีค่าความจริงตรงข้ามกัน
5. นิเสธของประพจน์
นิเสธของประพจน์ใดๆ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ
และสามารถเขียนแทนนิเสธของ p ได้ด้วย ~p
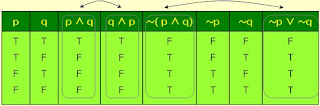
ตารางแสดงค่าความจริงของประพจน์ที่มีตัวเชื่อม

ประพจน์ที่สมมูลกันและเป็นนิเสธกัน
ประพจน์ที่สมมูลกัน
ประพจน์ 2 ประพจน์จะสมมูลกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงเหมือนกัน ทุกกรณีของค่าความจริงของประพจน์ย่อย
ตัวอย่างประพจน์ที่สมมูลกันที่ควรทราบ มีดังนี้
p ∧ q สมมูลกับ q ∧ p
p ∨ q สมมูลกับ q ∨ p
p ∧ q) ∧ r สมมูลกับ p ∧ (q ∧ r)
p ∨ q) ∨ r สมมูลกับ p ∨ (q ∨ r)
p ∧ (q ∨ r) สมมูลกับ (p ∧ q) ∨ ( p ∧ r)
p ∨ (q ∧ r) สมมูลกับ (p ∨ q) ∧ ( p ∨ r)
p → q สมมูลกับ ~p ∨ q
p → q สมมูลกับ ~q → ~p
p ⇔ q สมมูลกับ (p → q) ∧ (q → p)
ประพจน์ที่เป็นนิเสธกัน
ประพจน์ 2 ประพจน์เป็นนิเสธกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงตรงข้ามกันทุกกรณีของค่าความจริงของประพจน์ย่อย
ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้
~(p ∧ q) สมมูลกับ ~p ∨ ~q
~(p ∨ q) สมมูลกับ ~p ∧ ~q
~(p → q) สมมูลกับ p ∧ ~q
~(p ⇔ q) สมมูลกับ (p ⇔ ~q) ∨(q ⇔ ~p)
~(p ⇔ q) สมมูลกับ (p ∧ ~q) ∨ ( q ∧~p)
สัจนิรันดร์
ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริง ทุกกรณีของประพจน์ย่อย
ตัวอย่างประพจน์ที่เป็นสัจนิรันดร์ที่ควรทราบ มีดังนี้
p ∨ ~q [ ~p ∧ ( p ∨ q)] → q
~(p ∧ ~q) [ ( p → q) ∧ ~q ] → ~p
(p ∧ q) → p (p ∧ q) ⇔ (q ∧ p)
(p ∧ q) → q (p ∨ q) ⇔ (q ∨ p)
p → (p ∨ q) (p → q) ⇔ (~p ∨ q)
q → (p ∨ q) (p → q) ⇔ (~q → ~p)
[ p ∧ ( p → q)] → q (~p ∨ q) ⇔ (~q → ~p)
[ ~p ∧ ( p → q)] → ~q ( p ⇔ q) ⇔ [(p → q) ∧ (q → p)]
ข้อสังเกต ประพจน์ที่สมมูลกัน เมื่อนำมาเชื่อมด้วยตัวเชื่อม ⇔ จะได้ประพจน์ใหม่ซึ่งเป็นสัจนิรันดร์ นั่นคือ ถ้า A และ B สมมูลกันแล้ว A ⇔ B เป็นสัจนิรันดร์
พิสูจน์


ประโยคเปิด
บทนิยาม ประโยคเปิด คือ ประโยคบอกเล่า หรือประโยคปฏิเสธที่ประกอบด้วยตัวแปรทำให้ไม่เป็นประพจน์ และเมื่อแทนที่ตัวแปรด้วยสมาชิกในเอกภพสัมพัทธ์แล้วจะได้ประพจน์
เราสามารถเขียนแทนประโยคเปิดที่ประกอบด้วยตัวแปร x ด้วยสัญลักษณ์ P(x) หรือ Q(x) และเขียนแทนประโยคเปิดที่ประกอบด้วยตัวแปร x และ y ด้วยสัญลักษณ์ P(x,y) หรือ Q(x,y)
ตัวอย่างเช่น
• เขาเป็นคนดี ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “เขา”
• x > 3 ⇒ เป็นประโยคเปิดที่ประกอบด้วยตัวแปร “x”
ตัวบ่งปริมาณ
ตัวบ่งปริมาณ เป็นตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ
1. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกทุกตัวในเอกภพสัมพัทธ์”
ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∀” อ่านว่า”สำหรับสมาชิก x ทุกตัว”
2. ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกบางตัวในเอกภพสัมพัทธ์
ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∃” อ่านว่า “สำหรับสมาชิก x บางตัว”
ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ
1. ∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง
2. ∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ
3. ∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง
4. ∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง
นิเสธของประพจน์ที่มีตัวบ่งปริมาณ
~∀x[P(x)] สมมูลกับ ∃x[~P(x)]
~∃x[P(x)] สมมูลกับ ∀x[~P(x)]
~∀x[~P(x)] สมมูลกับ ∃x[P(x)]
~∃x[~P(x)] สมมูลกับ ∀x[P(x)]
ตัวอย่างเช่น
• ∀x[x < 0] เมื่อ u = เซตของจำนวนเต็ม
มีค่าความจริงเป็นเท็จ เพราะเมื่อแทน x เป็นจำนวนเต็มบวกและศูนย์ จะทำให้ x < 0 เป็นเท็จ
• ∃x[x < 0]เมื่อ u = เซตของจำนวนเต็ม
มีค่าความจริงเป็นจริง เพราะเมื่อแทน x เป็นจำนวนเต็มลบ จะทำให้ x < 0 เป็นจริง
การอ้างเหตุผล
การอ้างเหตุผล คือ การอ้างว่า "สำหรับเหตุการณ์ P1, P2,..., Pn ชุดหนึ่ง สามารถสรุปผลที่ตามมา C ได้"
การอ้างเหตุผลประกอบด้วย 2 ส่วน คือ
1. เหตุ หรือสิ่งที่กำหนดให้
2. ผล หรือสิ่งที่ตามมา
สำหรับการพิจารณาว่า การอ้างเหตุผลนั้นสมเหตุสมผลหรือไม่นั้นพิจารณาได้จากประพจน์ ( P1 ∧ P2 ∧ ... Pn) → C ถ้าประพจน์ดังกล่าวมีค่าความจริงเป็นจริงเสมอ (เป็นสัจนิรันดร์) เราสามารถสรุปได้ว่าการอ้างเหตุผลดังกล่าวเป็นการอ้างที่สมเหตุสมผล
ตัวอย่างเช่น
เหตุ 1. p → q
2. p
ผล q
